•Solução-3
De acordo com as regras definidoras, conclui-se que
Portanto, os diferentes elementos de 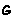 são:
são:
Comprimento 1: 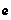 ,
, 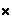 ,
, 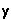
Comprimento 2: 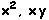 ,
, 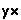
Comprimento 3: 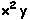 ,
, 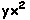 ,
, 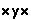 ,
, 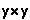
Comprimento 4: 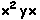 ,
, 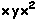 (O elemento
(O elemento 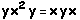 já foi contabilizado.)
já foi contabilizado.)
O grupo não possui elementos de comprimento 5 porque 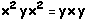 e
e 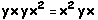 .
.
Os pares de elementos inversos são:
Observe que estes pares têm de estar juntos dentro ou fora de cada subgrupo de 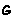 . Além disso, os subgrupos têm que ter cardinalidade divisora de
. Além disso, os subgrupos têm que ter cardinalidade divisora de ![!4[G] = 12](../HTMLFiles/index_105.gif) . Assim, procuremos subgrupos próprios de ordem
. Assim, procuremos subgrupos próprios de ordem 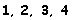 e
e 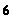
Não existe subgrupo de ordem 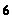 .
.
A determinação de um subgrupo normal pode teóricamente ser feita através do comutador ![[G, G] = < [g, g^'] = g g^'(g^' g)^(-1) > _ (g ∈ G)](../HTMLFiles/index_117.gif) . O subgrupo gerado por este espaço é
. O subgrupo gerado por este espaço é  porque, se
porque, se ![n ∈ [G, G]](../HTMLFiles/index_119.gif) , então
, então 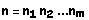 onde cada
onde cada 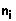 é da forma
é da forma 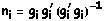 . Como a conjugação é distributível em relação ao produto, basta mostrar que, para
. Como a conjugação é distributível em relação ao produto, basta mostrar que, para 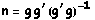 e
e 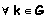 ,
, ![k n k^(-1) = k (g g^' (g^' g)^(-1)) k^(-1) = Overscript[g, ~] Overscript[g, ~]^'(Overscript[g, ~]^' Overscript[g, ~])^(-1)](../HTMLFiles/index_125.gif) onde
onde ![Overscript[g, ~] = (k g k^(-1))](../HTMLFiles/index_126.gif) e análogamente para
e análogamente para ![Overscript[g, ~]^'](../HTMLFiles/index_127.gif) .
.
Mas na prática torna-se mais fácil determinar subgrupos que sejam soma directa de classes de conjugação completas de 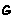 .
.
A tabela de multiplicação de classes é
O único candidato é 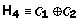 já que
já que 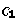 e
e 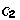 são as únicas classes contêm os próprios inversos e cujo produto é fechado.
são as únicas classes contêm os próprios inversos e cujo produto é fechado.
Mathematica
Converted by Mathematica
(October 16, 2002)
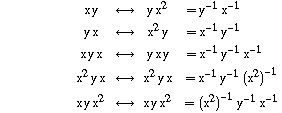
![]() . Além disso, os subgrupos têm que ter cardinalidade divisora de
. Além disso, os subgrupos têm que ter cardinalidade divisora de ![]() . Assim, procuremos subgrupos próprios de ordem
. Assim, procuremos subgrupos próprios de ordem ![]() e
e ![]()